1 静定はりのsfdとbmd 11 例題1集中荷重を受ける両端単純支持はり 図1 に示すはりのsfd、bmd を求めなさい。 p54 有限要素の特徴 Up 5 仮想仕事の原理と有限要素法の基礎 Previous 52 有限要素法の基礎 最新版を正確に読む場合には pdf ファイル をどうぞ。 これは web 検索のための簡易旧版です。1次不静定 2次不静定 3次不静定 単純梁 片持梁 1 1 (復習) 安定・不安定と静定・不静定の確認 3 静定・不静定 • 力のつりあい条件だけで決まる → 静定 –支点反力が決まる→外的静定 –部材応力が決まる→内的静定 • つりあい条件だけで決まらない
種々のはりのたわみ
両端固定梁 不静定
両端固定梁 不静定- 不静定問題の見分け方 静定問題と不静定問題の見分け方にはコツがあります。 不静定問題としてあげられるものは、 「材料を固定している箇所が多いもの」 「材料が並列で並んでいるもの」 が多いです。 具体例をあげると、1) 各柱の支持方法をチェック(「固定固定」or「固 定ピン」) 2) 「固定固定」の場合は、柱の中心で2等分し、2 本の片持ち梁として水平変位(梁のたわみ)を求 める 3) 「固定ピン」の場合は、柱全体が1本の片持ち梁 であるとして水平変位を求める



この両端固定梁の曲げモーメント図を数値の出し方も含めて教えてくださ Yahoo 知恵袋
不静定梁 / p (0050jp2) 両端固定梁の係数表 / p98 (0055jp2) 梁のタワミの公式 / p99 (0055jp2) 連続梁の公式 / p100 (0056jp2) 連続梁撓角法による公式 / p105 (0058jp2) 2,3,4スパン連続梁の公式 / p109 (0060jp2)ただし、1階梁の全塑性モーメント(M p)は、梁断面を b×D=250mm×550mm、降伏強度を240N/mm2 として 求めるものとする。 第6課題 不静定力学Ⅱ・同演習 第12回演習問題 3P M p 07M p 08M p M p M p M p 15M p 15M p M p 15M p 15M p 4m 4m 6m 6m 45m 2P P 崩壊メカニズム称 ローラー ピン 固定 特徴 一方向に並進可能 それと垂直方向は拘束 回転自由 移動拘束 回転自由 移動も回転も拘束 反力数 1 2 3 イメージ 記号 3次不静定 単純梁 片持梁 1 1 両端
不静定梁のたわみ その2 第 12 章 不静定梁のたわみ 12 1 その2 第12章 不静定梁のたわみ その2 ポイント:一端固定、一端ピン支持の梁の解析を行う 微分方程式の解析方法をより深く理解する 本章では、前章に続いて、不静定梁の応力解析を実施し、梁の基礎64話 不静定な基本構造の応力解析No2 1 構造力学 基礎の初歩 SPACE 前回の続きで、図4に示す両端固定支持梁に等分布荷重が加わる場合 の応力解析を行う。等分布荷重 p w を受ける梁の微分方程式は、 1 で与えられ、上の両辺を4回積分すると、 dx 32 1 2梁の不静定問題(1) 釣り合い式からだけでは反力を求められない問題(不静定問題)におけるたわみの算出法につ いて解説する. 10 梁の不静定問題(2) 前回に引き続き,不静定問題の解法について解説する. 11 面積モーメント法による梁のたわみの算出
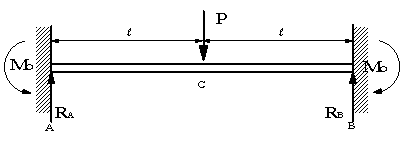
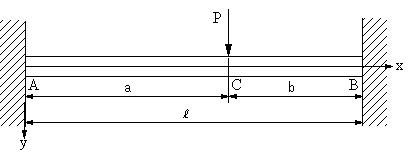
このことは静定ばりの場合にだけ言えることであり、不静定ばりでは異なることを図3 の様な両端を固定した不静定ばりの中央に集中荷重が作用している場合を例にして説明し よう。図3 の問題の解き方は教科書の6 章、図1の問題の解法過程あるいは9 章、例題8『解法16』不静定構造の応力 @本講座サブテキp46 過去問57図のような骨組に水平荷重100knが作用したとき、部材bcの引張力tは50knであった。このとき、柱 abのa点における曲げモーメントの絶対値を求めよ。139 静定と不静定 支点に生じる反力を力のつりあいの3条件で解けるものを静定梁、 力のつりあい条件だけでは解けないものを不静定梁といいます。 作用する荷重に対して、支点に生じる反力を求めること、 求めた反力により梁部材に生じる断面力 ・曲げ
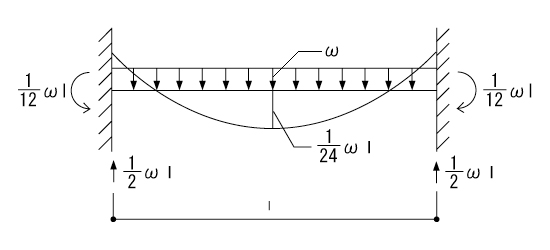



よくでる不静定モーメント 構造力学 Com
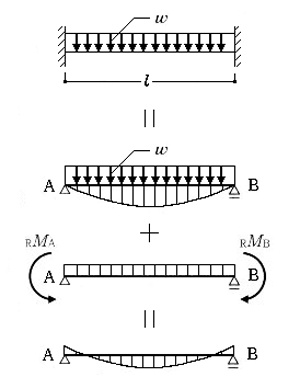



不静定ばりの応力解答 構造力学 Com
梁の微分方程式 不静的構造物の応力解析 一端固定他端ピン支持梁 本節では、図121に示す一端固定・一端ピン支持の不静定梁が等分 布荷重を受けるモデルを応力解析し、断面力の分布とたわみ曲線、ある いは最大曲げモーメントや最大変位を求める。図111 両端固定梁の解析モデル 変位と荷重には以下のような関係がある。 4 4 zw() dw EI P x dx = ここで、Pw()x は分布荷重であり、x の関数で ある。 ポイント:基本的な不静定梁のたわみ 梁部材の断面力とたわみ 第11章 不静定梁のたわみ 111 はじめに 112 不静定定する。 固定モーメントまたは不釣合モーメントと呼ぶ まず,各要素では,要素内に荷重が加わっているため,要素両端の固定端モーメントが 計算できます。 固定端モーメントは,たわみ角法の時に勉強したように,要素両端の回転角を0にした



両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方




静定構造と不静定構造の実建物における違い 力学と実現象の架け橋 バッコ博士の構造塾
不静定骨組みの各部材の端部に作用する モーメント(材端モーメント)を、部材端部の変 形角と、部材角、固定端モーメントを用いて表 し、釣合いより連立方程式を解いて、変形角、 部材角を求め、材端モーメントを求める方法。 基本仮定 部材は線材置換固定端bに強制変位Δを受ける不静定はりについて、たわみとたわみ角の関数を求めよ。 但し、曲げ剛性をEIとし、これを一定の物 とする。 解決済み 質問日時: 008 回答数: 1 閲覧数: 338図7不静定 g 市固定梁'X 曲げモーメント図解答の例 3 調査結果および考察 31 誤答の中身 図6不静定・一端固定梁 l工たわみ解答の例 図3から図9に学生の誤った解答の例を示す。また表I に曲げモーメント (M) 図,引張応力点,たわみ形の解答 33 ←



固定端モーメントとは 1分でわかる意味 片持ち梁とc 両端固定梁



第8章 構造解析法への適用
静定はりと不静定はり 静定はり 未知変数、反力、固着モーメント 力のつりあい A点周りのモーメントのつりあい xの位置におけるせん断力 xの位置における曲げモーメント たわみの式 ←A点で固定: ←A点で固定: B点でのたわみ角iB B点でのたわみ B梁のタワミの公式 / p99 連続梁の公式 / p100 連続梁撓角法による公式 / p105 2,3,4スパン連続梁の公式 / p109 連続梁の反力,剪断力,曲げモーメントの公式 / p114 2,3,4スパン連続梁係数表 / p115 トラスの型式 / p118 トラス格点モーメント及剪断力係数表 / p119 曲弦両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが,この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。と が未知の不静定反力である。 等分布外力が作用した梁の 場合には,式()より



Http Msnb Sakura Ne Jp Mecha E6 81 81 Ae E6 9b B2 81 92 Pdf



両端固定梁のたわみ 応力 支持反力 集中荷重
図の両端支持はりの場合に、たわみの式を求める。 解答例 問題1 図の不静定梁の場合に、各支点における反力とたわみ角、たわみの式を求める。 解答例 問題2図の不静定の梁の場合に、たわみ曲線とA支点の反力を求める。 解答例 問題160 図の不静定梁の場合に、各支点における反力とたわみの式を求める。 解答例 問題161 長さ400mmの単純支持はりの中央に集中荷重Pが作用する。静定構造から不静定構造へ 34 静定構造解析が容易. 不同沈下に対して応力が生じない. 拘束条件が一つでも減ると崩壊する. 不静定構造 解析が比較的複雑.→コンピュータの発達で障害 なし. 不同沈下で応力が発生.→基礎構造の性能が重要.
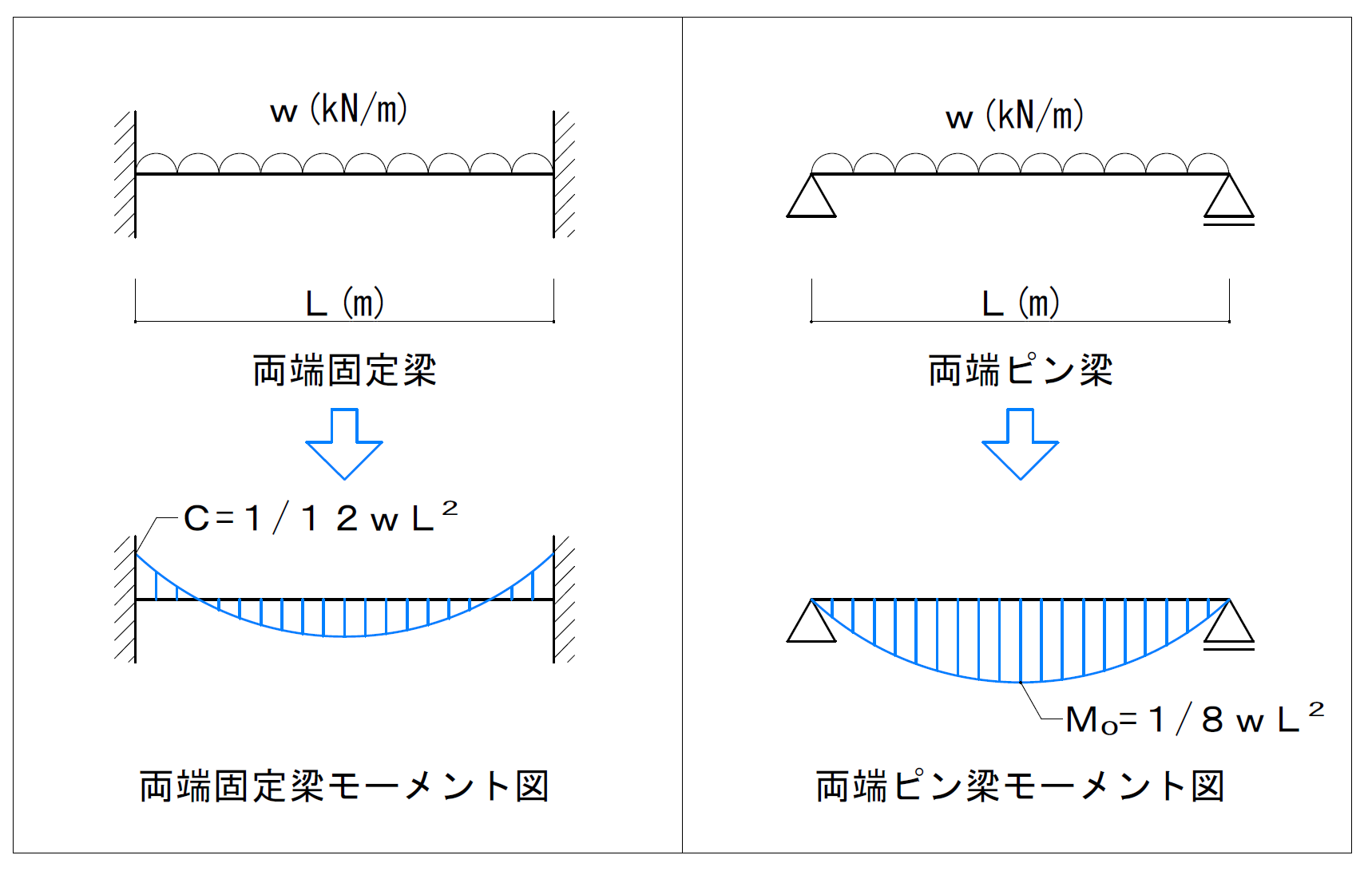



小梁の設計 C M Qとは 構造設計memo



連続はり
C116 講義資料 材料力学 Golden, CO, USA (09) 京都大学農学部地域環境工学科 中嶋 洋 Ver図52 静定ばり 突き上げ片持ばり 固定ばり 3 1 1 3 3 図53 不静定ばり 右回りを正とする 上向きを正とする 右向きを正とする a 点でモーメントをとる 表51 支点の種類と反力43 重ね合わせの原理で不静定梁を解く Tohoku University 両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが,この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。と が未知の不静定反力である。



Stage Tksc Jaxa Jp Taurus Member Miyazaki Old Lecture Strength Of Materials Ii 15 Pdf




二級構造 変形と不静定構造物 一級建築士 二級建築士に合格 建築センター公認の建築士試験過去問題無料解説サイト
構造力学の授業でまず習うのが「静定構造」、その次に習うのが「不静定構造」です。 疑問 「静定構造」と「不静定構造」が具体的にどういうものなのかわかりません。また、構造設計の際にどのように使い分けするのでしょうか。 回答 「静定構造」は力の釣り合いだけで解ける単純な構造(c) 一端固定他端支持はり (d) 両端固定はり 図12 はりの種類 日本マリンエンジニアリング学会執筆要項 Journal of the JIME Vol00,No00(05) -3- 日本マリンエンジニアリング学会誌 第00 巻 第00 号 (05) "不静定はり"と呼ぶ.静定はりでは,力とモーメン トの29 建築士 両端固定の等分布荷重の不静定梁を解く場合 (たわみ公式で言うと wl^4/384EIの不静定梁です) 端部モーメントは2つの静定梁に分けて それぞれのたわみ角θのプラスマイナス wl^3/
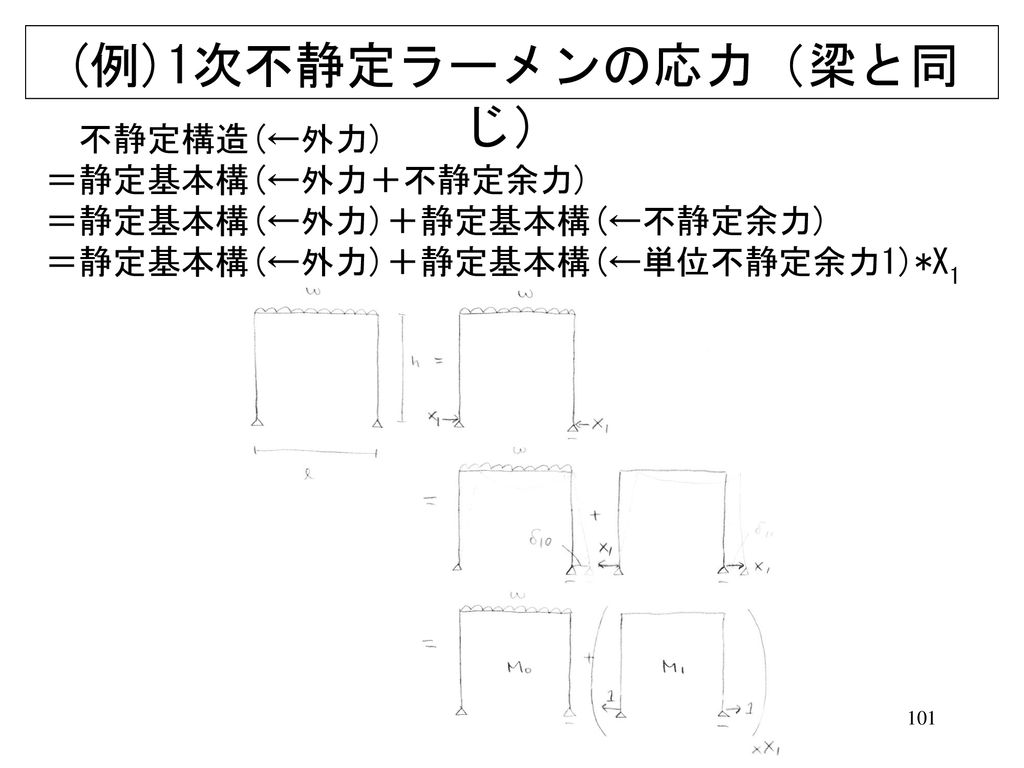



構造力学 シラバス 建築物 橋などの構造設計の際に必要となる トラス ラーメン などの構造 骨組 が Ppt Download
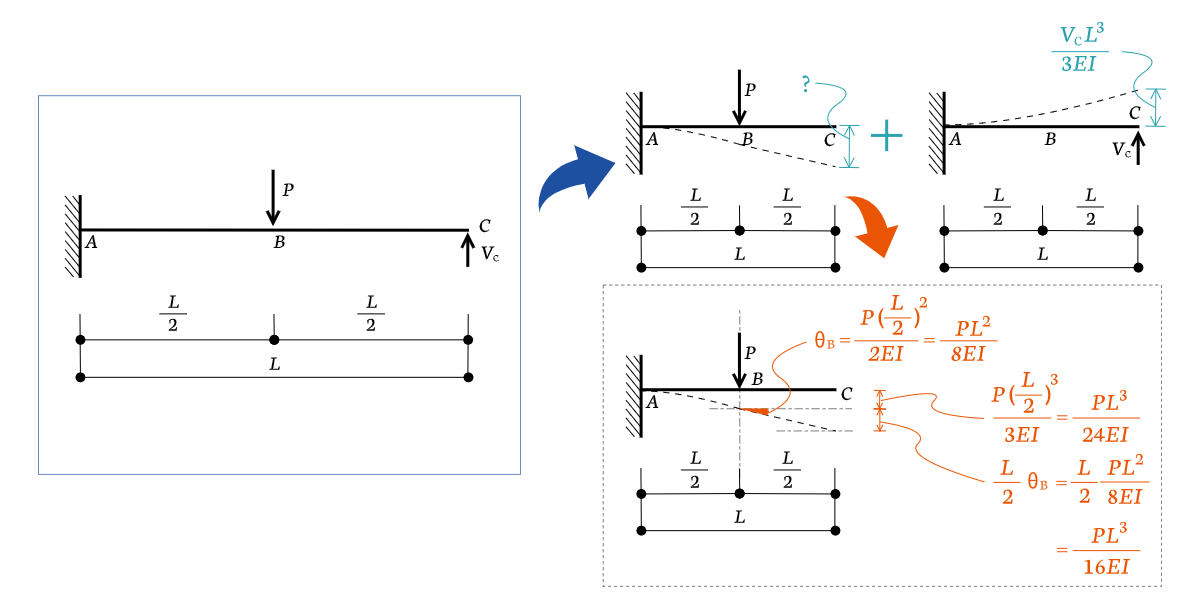



不静定構造をたわみ公式を使って解く方法を解説 ゆるっと建築ライフ
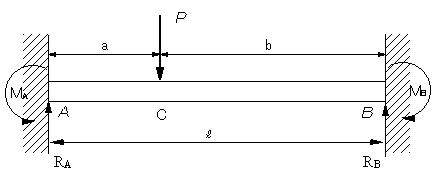
棒の引張・圧縮(不静定) 14.右図のように,変断面棒acb を剛壁間 に固定して,断面cに軸力pを作用させる.棒 acの断面積を a 1,長さを l a,棒cbの断面積を a 2,長さを bとする.棒acおよび棒cbのヤ ング率はともに eとする. 棒ac,棒cbに生じる応力例題:一端固定、他端単純支持梁 固定端曲げモーメントは? a b m b t0 1次不静定構造系故、古典的解法によれば、 不静定構造解析の手順に従い変形解析が必要 たわみ角法によれば、変形解析は必要なし。 b端固定支持、剛体回転及び中間外力無し。 q b =r
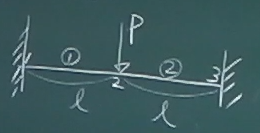



マトリクス構造解析 第6回
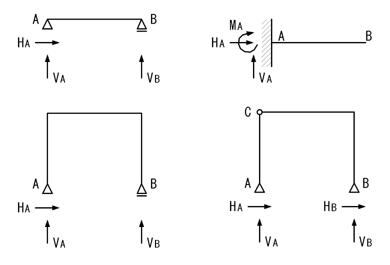



01 静定 不静定 合格ロケット



第11章 ラーメン理論



構造力学の質問です 画像の不静定次数を求める問題なので Yahoo 知恵袋




メルカリ 構造力学 考え方解き方 参考書 600 中古や未使用のフリマ



種々のはりのたわみ



材料力学についての質問です 不静定の両端固定梁のたわみ曲線を Yahoo 知恵袋



梁の種類や記号は 静定梁と不静定梁の違いについて解説 建築学科のための材料力学



5569et Com Wp Content Uploads 12 16 Fuseiteidannmenn Red Pdf




静定梁 せいていばり ってなに いまさら訊けない建築構造力学




図解レクチャー 構造力学 静定 不静定構造を学ぶ 浅野清昭 著 まち座 今日の建築 都市 まちづくり



Step1 1



不静定梁とは 1分でわかる意味 解き方 重ね合わせの原理 例題



種々のはりのたわみ



5569et Com Wp Content Uploads 12 16 Fuseiteidannmenn Red Pdf
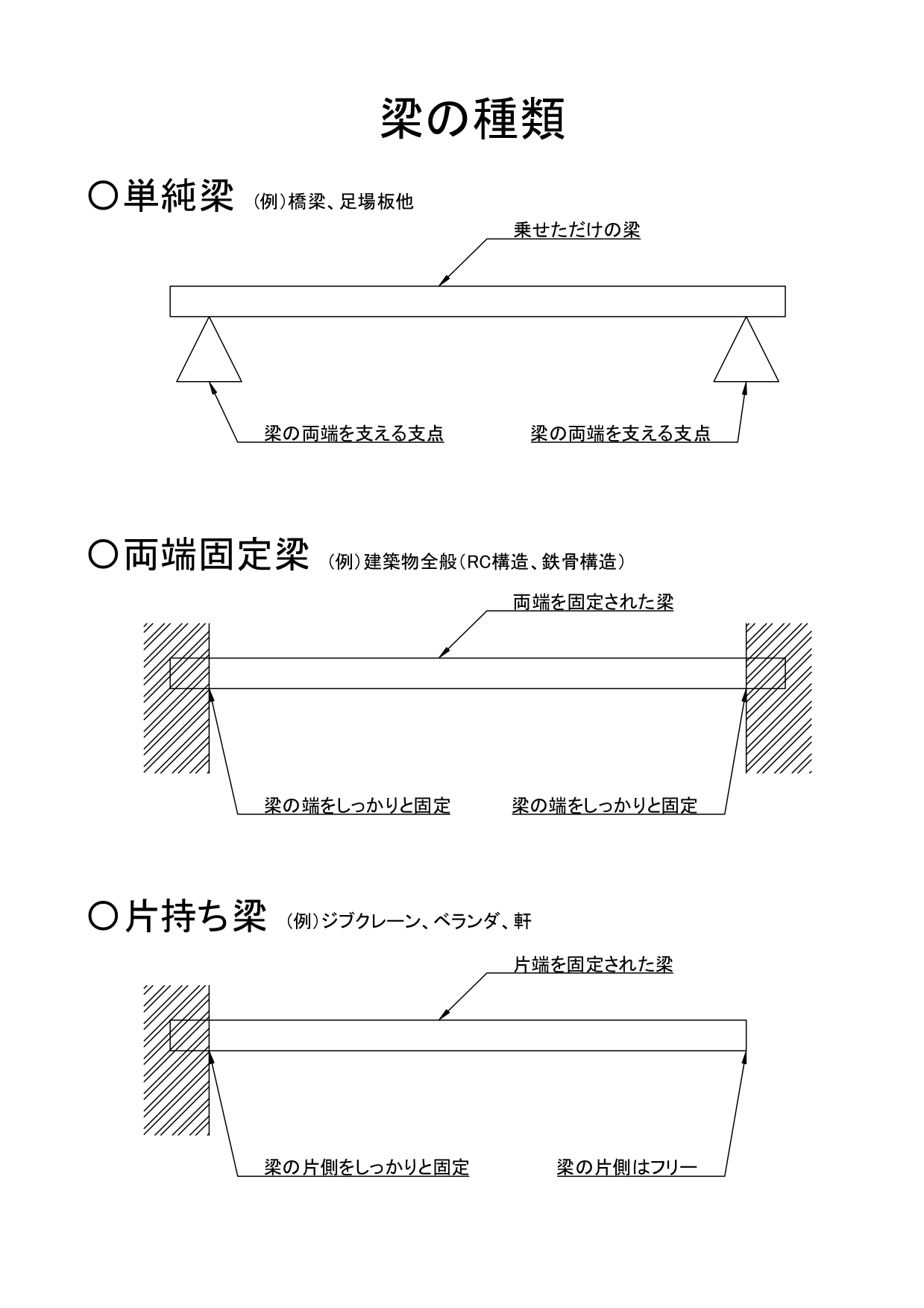



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



Http Wwwra Meijo U Ac Jp Labs Ra007 Murata Pdf Textbook Hari 11 Pdf



両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方




図解レクチャー 構造力学 静定 不静定構造を学ぶ 浅野清昭 著 まち座 今日の建築 都市 まちづくり



Ex 5




M Sudo S Room 両端支持梁 固定梁の任意の位置のたわみ



第8章 構造解析法への適用



Ex 5



Http Tass2x4 Sakura Ne Jp Sblo Files Tass2x4 Image E59fbae7a48e 64e8a9b1efbcbfe4bde99d99e5ae9ae381aae59fbae69cace6a78be980a0e381aee5bf9ce58a9be8a7a3e69e90no2 Pdf



種々のはりのたわみ




リフォームブックス 図解レクチャー 構造力学 静定 不静定構造を学ぶ B5変型0頁



4 3 重ね合わせの原理で不静定梁を解く



Ex 5



両端固定梁



この両端固定梁の曲げモーメント図を数値の出し方も含めて教えてくださ Yahoo 知恵袋



種々のはりのたわみ



4 3 重ね合わせの原理で不静定梁を解く



不静定梁を固定モーメント法で解く方法



単純梁 全23頁pdf版 建築学生が学ぶ構造力学 Booth




材料力学静定梁両端固定の最大たわみ 材料力学の静定梁の問題です 両端固定 Okwave
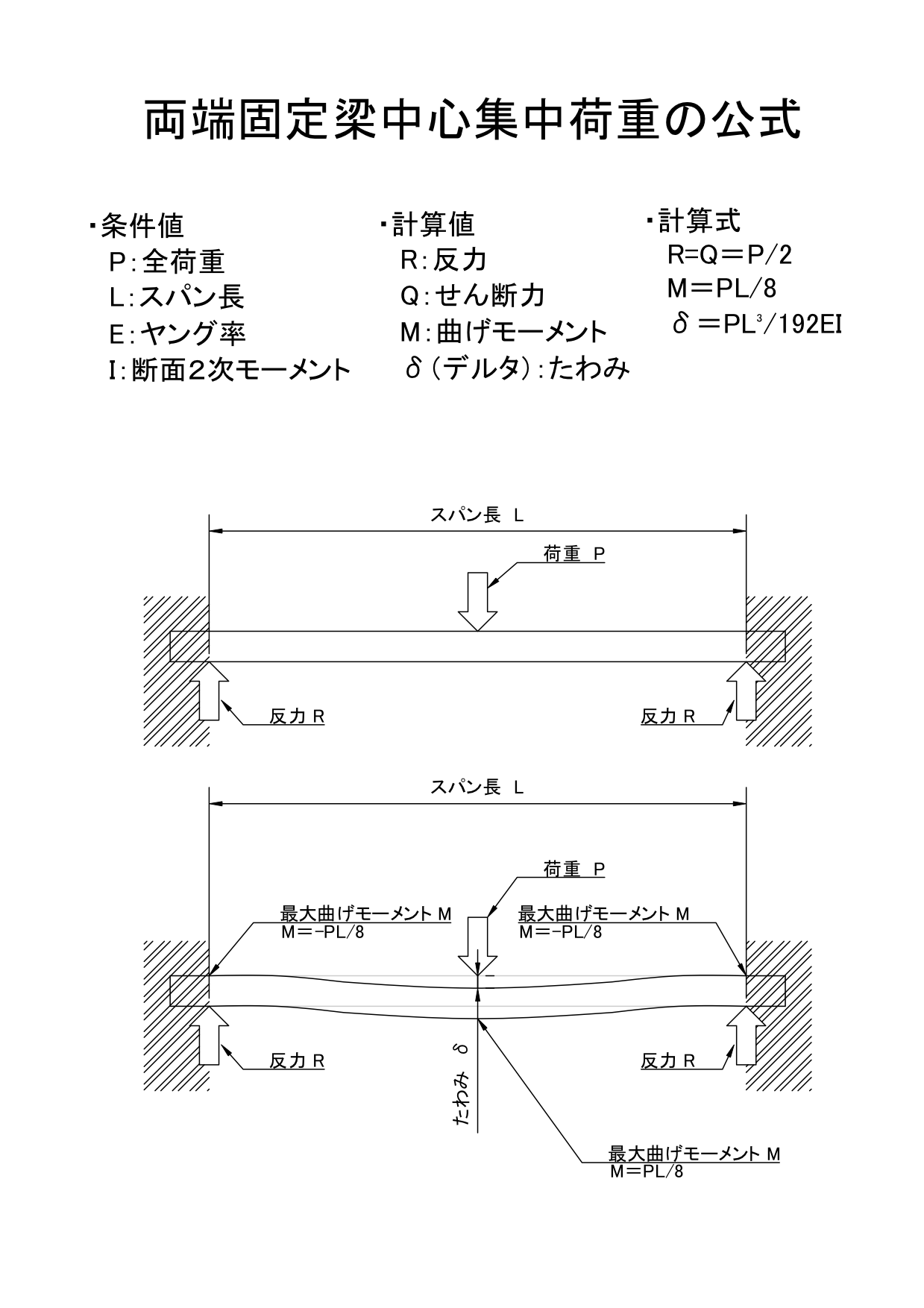



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督
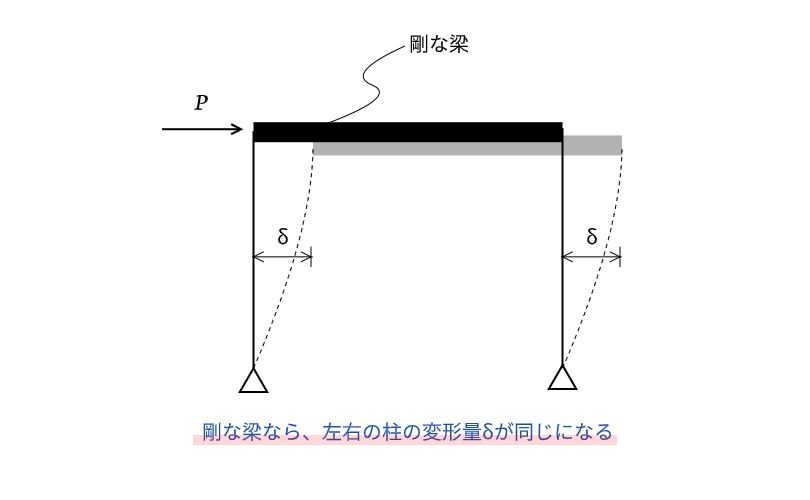



構造力学 水平剛性の問題の解き方を解説 ゆるっと建築ライフ




梁の計算4 両端固定梁 集中荷重 1 Youtube



Stage Tksc Jaxa Jp Taurus Member Miyazaki Old Lecture Strength Of Materials Ii 15 Pdf



不静定構造物の不静定力算出に関する質問です 画像の問題で a点での不 Yahoo 知恵袋
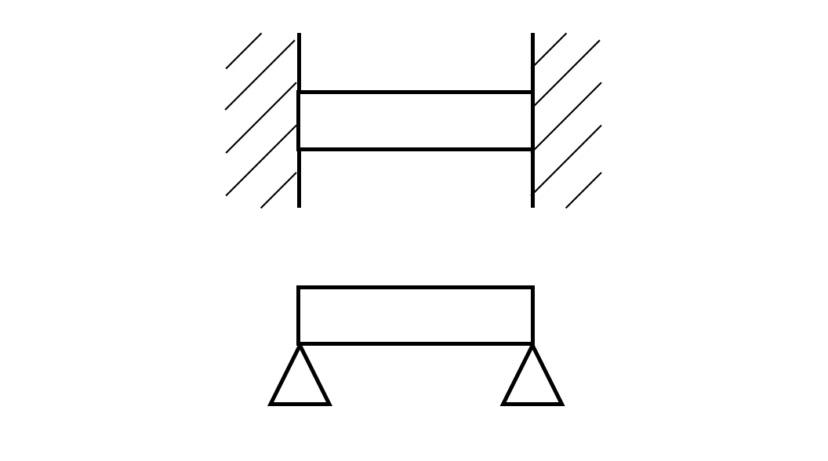



梁の支持方法と 使い分けの方法 ものづくりのススメ




M Sudo S Room 不静定梁の解法例



4 1 梁の境界値問題
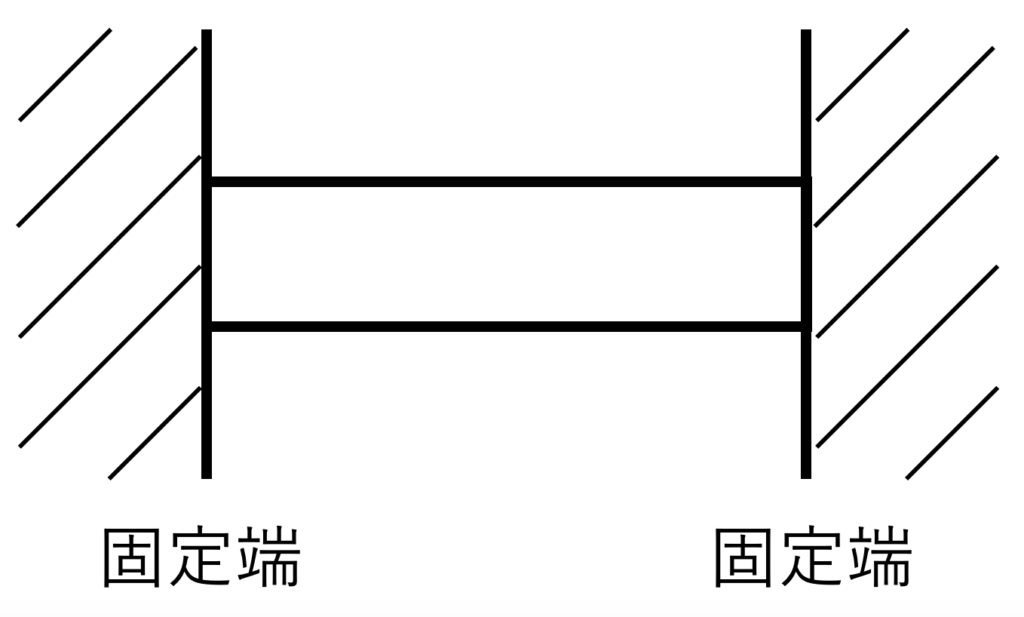



梁の支持方法と 使い分けの方法 ものづくりのススメ



第8章 構造解析法への適用



Step1 1
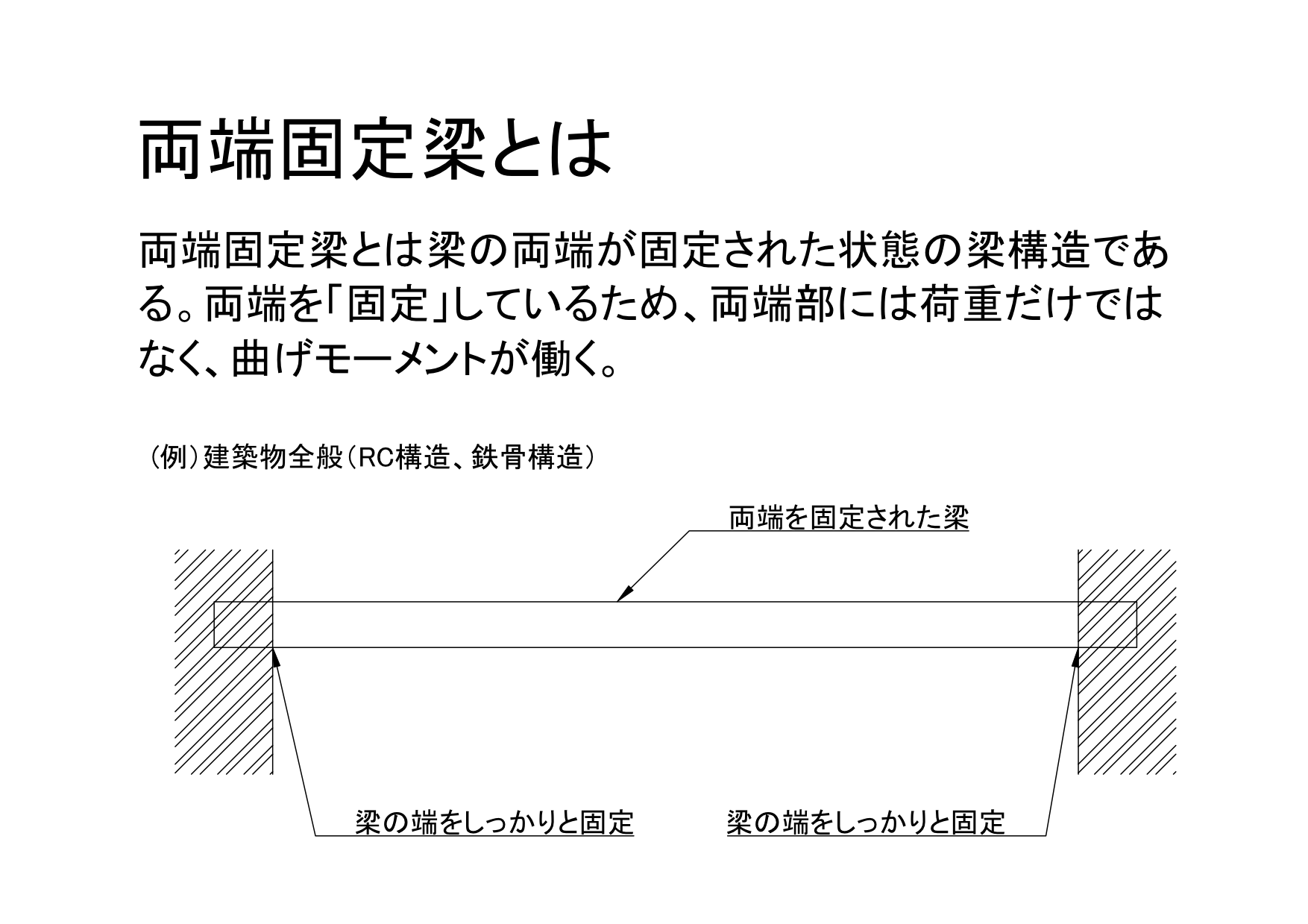



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



2



2




両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断 工学 教えて Goo




静定梁 せいていばり ってなに いまさら訊けない建築構造力学




構造力学 シラバス 建築物 橋などの構造設計の際に必要となる トラス ラーメン などの構造 骨組 が Ppt Download
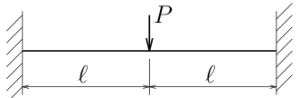



構造力学 不静定梁のたわみ 練習問題




M Sudo S Room 両端支持梁 固定梁の任意の位置のたわみ



4 3 重ね合わせの原理で不静定梁を解く
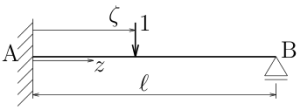



構造力学 不静定梁の影響線




一級建築士試験で覚えておくたわみとたわみ角の覚え方 建築士試験の勉強法




1級建築士試験 構造力学 分割モーメントと水平剛性の問題 1級建築士 ワンワンの建築世界



不静定はり に関するq A Yahoo 知恵袋
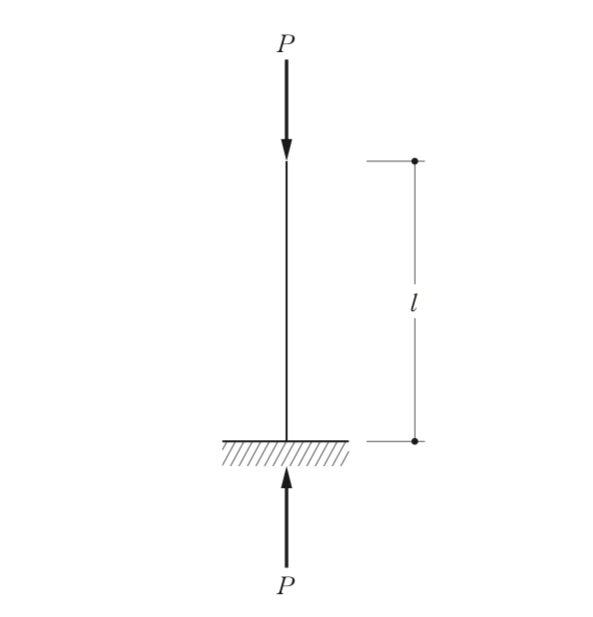



二級構造 変形と不静定構造物 一級建築士 二級建築士に合格 建築センター公認の建築士試験過去問題無料解説サイト



梁の種類や記号は 静定梁と不静定梁の違いについて解説 建築学科のための材料力学



両端固定梁のたわみ 応力 支持反力 集中荷重
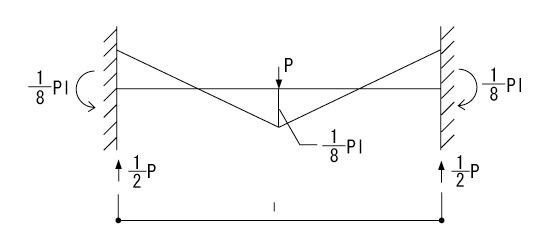



よくでる不静定モーメント 構造力学 Com



Excelを使った数値計算ツールsuitexl



2



はりの話 前編




材料力学の不静定問題について 図2 17 添付データ に示すように 長さ Okwave



不静定次数を計算して 不安定 静定 不静定を判別する方法 今日 建築やめてきた
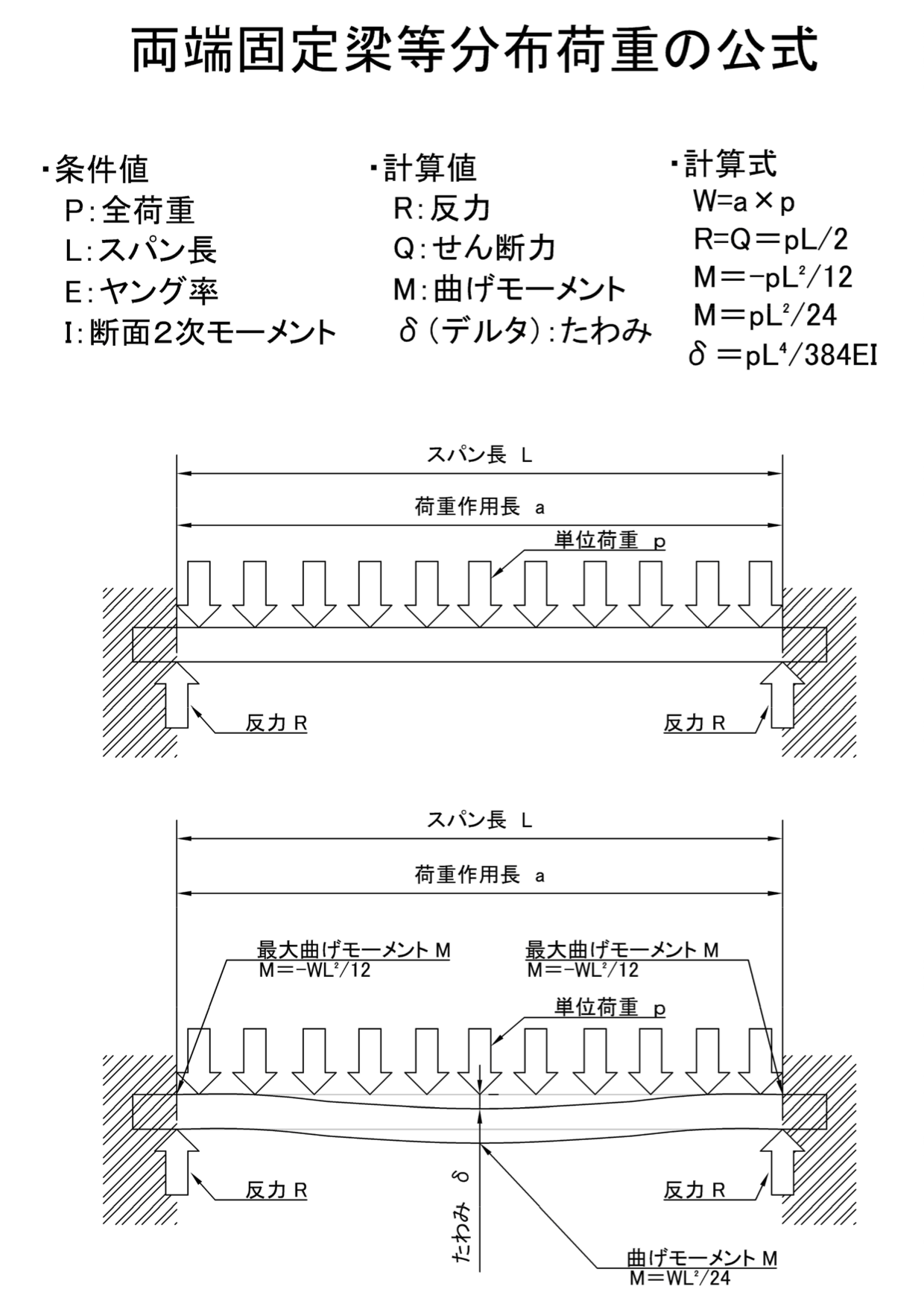



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



不静定次数を計算して 不安定 静定 不静定を判別する方法 今日 建築やめてきた




梁の公式集 理工図書株式会社



4 3 重ね合わせの原理で不静定梁を解く



Http Wwwra Meijo U Ac Jp Labs Ra007 Murata Pdf Textbook Hari 12 Pdf



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算



Http Wwwra Meijo U Ac Jp Labs Ra007 Murata Pdf Textbook Hari 11 Pdf




梁の計算7 両端固定梁 等分布荷重 Youtube
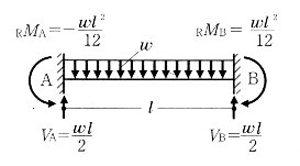



不静定ばりの応力解答 構造力学 Com



Shake Tu Chiba U Ac Jp Lecture Strmcni Pdf Stri Note 04 Pdf



連続はり
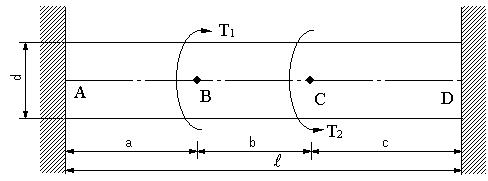



Ex 5



Ex 6



Http Sd40c3ac5152ec7 Jimcontent Com Download Version Module Name E5 9b Ba E5 Ae 9a E6 95 Pdf



Ex 8



4 1 梁の境界値問題



第8章 構造解析法への適用



連続はり



0 件のコメント:
コメントを投稿